Artificial intelligence is rapidly transforming various fields, and geometry is no exception. This guide provides a comprehensive overview of how AI can be used to solve geometry problems, from basic to complex. We will explore diverse AI techniques and tools, examining how they approach different types of geometric challenges, and ultimately, understanding the potential of AI in geometry education.
The guide will delve into the various types of geometry problems AI can tackle, including coordinate geometry, Euclidean geometry, and more. It will also Artikel the different AI tools and techniques that can be applied to solve these problems, such as machine learning and deep learning algorithms. This detailed approach ensures a clear understanding of how AI can aid in geometry problem-solving.
Introduction to AI in Geometry Problem Solving
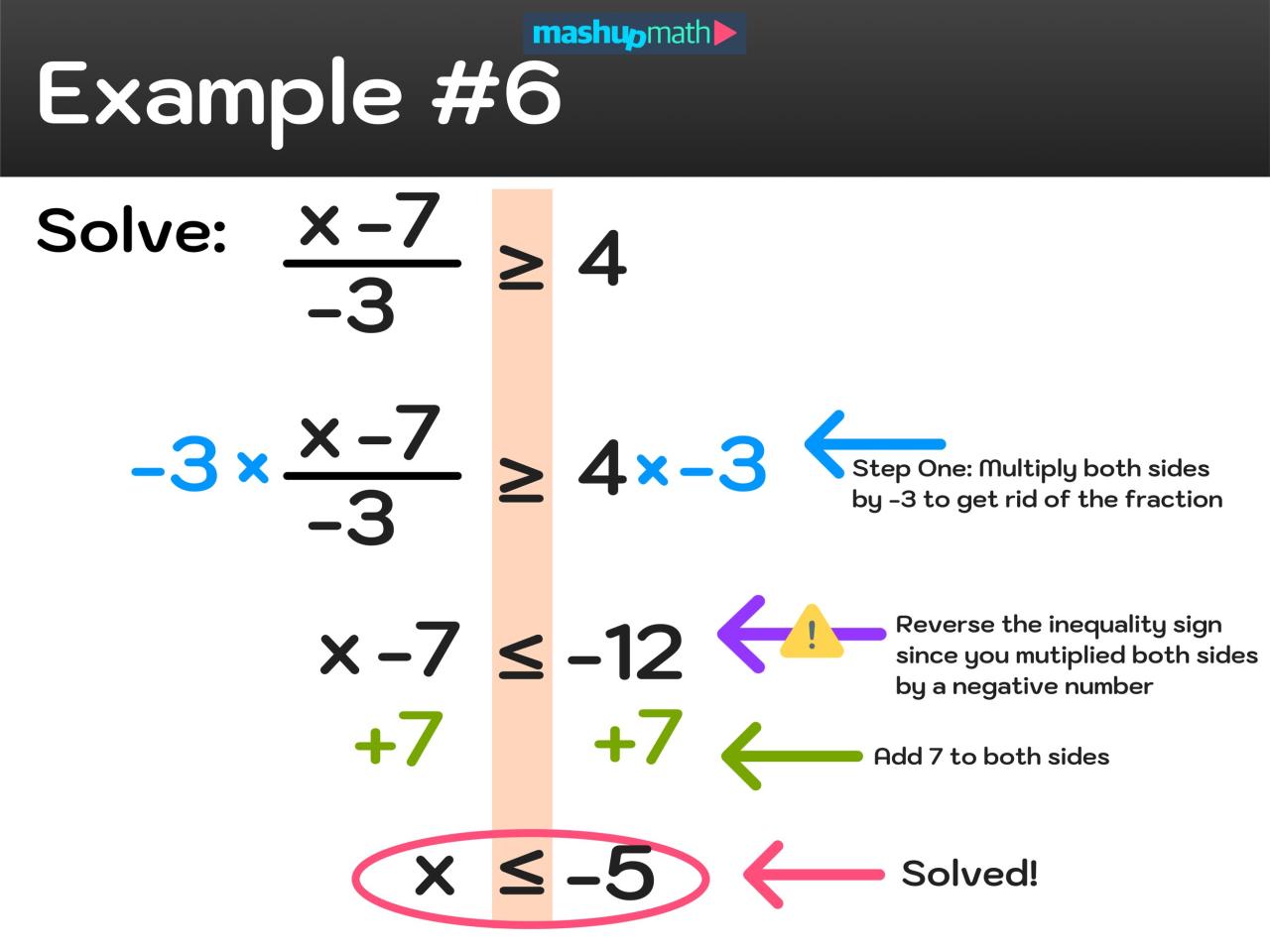
Artificial intelligence (AI) is rapidly transforming various fields, and geometry is no exception. AI techniques offer powerful tools to approach geometry problems, automating complex calculations and facilitating deeper insights. This allows for the analysis of intricate geometric shapes and patterns, leading to more efficient problem-solving strategies.AI excels at handling large datasets and complex algorithms, making it well-suited for identifying patterns and relationships within geometric structures.
This capability extends to various types of geometry problems, from straightforward coordinate geometry to advanced Euclidean geometry. The application of AI techniques in geometry promises a paradigm shift in how we approach and understand geometric concepts.
Different Types of Geometry Problems AI Can Handle
AI can address a wide range of geometric problems. These problems span different areas of geometry, including coordinate geometry, Euclidean geometry, and more specialized branches. Coordinate geometry, involving points, lines, and curves on a coordinate plane, is particularly amenable to AI-driven analysis. Euclidean geometry, focusing on axioms and theorems in two and three dimensions, also benefits from AI’s ability to process intricate relationships.
AI Techniques for Geometry Problem Solving
Several AI techniques can be effectively applied to solve geometry problems. Machine learning (ML) algorithms can identify patterns and relationships within geometric data, enabling prediction and classification of geometric shapes and properties. Deep learning (DL), a more sophisticated form of ML, leverages neural networks to extract intricate features and solve complex geometry problems.
Examples of AI Applications in Geometry
| Problem Type | AI Technique | Example Geometry Problem |
|---|---|---|
| Coordinate Geometry | Machine Learning | Predicting the coordinates of a point on a line based on given data points. |
| Euclidean Geometry | Deep Learning | Determining the area of a complex polygon defined by a set of coordinates using neural networks. |
| 3D Geometry | Machine Learning | Classifying different types of 3D shapes based on their geometric features. |
| Geometric Transformations | Deep Learning | Determining the transformation (rotation, translation, scaling) applied to a geometric figure. |
AI Tools for Geometry Problem Analysis
AI tools offer a powerful approach to analyzing geometry problems, augmenting human capabilities in problem-solving. These tools can efficiently identify key elements, relationships, and potential solution paths, significantly accelerating the problem-solving process. They leverage sophisticated algorithms and machine learning techniques to interpret complex geometric statements and translate them into a format suitable for automated analysis.AI tools can significantly aid in the understanding of geometric problems.
By breaking down complex problems into simpler components, AI can facilitate a systematic approach, ultimately improving the efficiency and effectiveness of the problem-solving process. This involves not just recognizing shapes and angles, but also extracting implicit information and relationships within the problem statement. This detailed analysis paves the way for a more comprehensive understanding, leading to more accurate and optimized solutions.
Process of Analyzing Geometry Problem Statements
AI tools employ a multi-step process to analyze geometry problem statements. This process begins with the tool receiving the problem statement in a structured format, such as text or a diagram. The tool then utilizes natural language processing (NLP) techniques to extract key elements and relationships from the text. Geometric shapes, their properties, and relationships between them are identified and categorized.
Following this, the tool utilizes pattern recognition to classify the problem type, determining whether it’s a problem involving triangles, quadrilaterals, circles, or other geometric figures. Finally, the tool analyzes the relationships between the identified elements, looking for connections and patterns that could lead to a solution.
Methods for Identifying Key Elements and Relationships
AI tools employ several methods to identify key elements and relationships within geometry problems. These methods include:
- Natural Language Processing (NLP): NLP algorithms parse the problem statement, identifying words and phrases associated with geometric figures, properties, and relationships. For example, words like “parallel,” “perpendicular,” “bisector,” or “congruent” are crucial for understanding the relationships between elements.
- Image Recognition (for diagram-based problems): If the problem includes a diagram, AI tools can use image recognition to extract geometric elements, such as points, lines, angles, and lengths. The tool can identify the relationships between these elements based on their position and intersection.
- Pattern Recognition: AI algorithms can identify patterns and relationships in the problem that may not be explicitly stated. For example, identifying similar triangles or recognizing specific theorems based on the given information. This is particularly valuable for more complex problems.
Breaking Down Complex Problems into Simpler Parts
AI tools can break down complex geometry problems into simpler, more manageable parts. This approach facilitates a step-by-step solution strategy.
- Decomposition: The tool decomposes the problem into smaller, more focused sub-problems. For example, a problem involving a complex polygon can be broken down into smaller problems involving triangles or quadrilaterals.
- Relationship Extraction: The tool extracts relationships between the sub-problems and the overall problem, highlighting how the solutions to the sub-problems contribute to the solution of the main problem.
- Simplification: The tool simplifies the sub-problems by identifying any inherent symmetries or redundant information, reducing the complexity to a manageable level.
AI Tools and Applications
The following table illustrates different AI tools and their applications in geometry problem-solving.
| Tool Name | Function | Example Application |
|---|---|---|
| Natural Language Processing (NLP) Engine | Extracts key information from problem statements (textual form). | Identifying the type of triangle (e.g., equilateral, isosceles) based on given properties. |
| Computer Vision Engine | Extracts geometric elements from diagrams (visual form). | Measuring lengths of segments and angles based on provided diagram. |
| Machine Learning Model (Geometry Theorem Recognition) | Identifies applicable theorems based on extracted information. | Determining the best theorem to use in a problem involving similar triangles. |
| Automated Reasoning Engine | Derives intermediate conclusions and relationships. | Deduce the value of an unknown angle based on the identified theorem. |
AI-Assisted Problem-Solving Strategies
AI can significantly enhance the process of solving geometry problems by leveraging its analytical capabilities and vast knowledge base. This approach allows for the exploration of diverse strategies and the identification of optimal solutions. It goes beyond simply providing answers; AI can explain the reasoning behind its choices, fostering a deeper understanding of geometric principles.AI’s ability to process complex geometric information and identify patterns enables it to suggest multiple approaches to problem-solving, even for seemingly intractable problems.
This multifaceted approach not only provides a wider range of potential solutions but also aids in understanding the relationships between different strategies.
AI Strategies for Different Geometry Problem Types
AI can adapt its problem-solving strategies based on the specific type of geometry problem. For example, problems involving coordinate geometry might benefit from algebraic manipulation and graphical representation, while problems involving Euclidean geometry might rely on theorems and postulates. This adaptability is crucial for handling the diverse range of geometry problems encountered in various contexts.
Generating Multiple Approaches
AI can generate multiple problem-solving strategies for a single geometry problem. This is achieved through its ability to identify various theorems, postulates, and properties that are applicable to the given problem. For instance, a problem involving the area of a triangle might be approached using the formula based on base and height, or through the use of Heron’s formula.
This flexibility allows for the exploration of different perspectives and potentially identifies the most efficient solution path.
Comparing and Contrasting Strategies
AI can analyze and compare different problem-solving methods for a given geometry problem. This analysis involves comparing the complexity of each method, the required steps, and the potential accuracy of the results. For example, an AI might identify that using the Pythagorean theorem is more straightforward than employing the law of cosines in a right triangle problem. This comparison assists in selecting the most appropriate strategy based on the given context.
Table of Examples
| Problem Statement | AI-Generated Strategies | Solution |
|---|---|---|
| Find the area of a triangle with vertices (1, 1), (4, 5), and (7, 2). |
|
The area is 8 square units. |
| Prove that the sum of the angles in a triangle is 180 degrees. |
|
The proof involves extending one side of the triangle and applying properties of parallel lines and angles. |
| Calculate the length of the hypotenuse of a right-angled triangle with legs of length 3 and 4. |
|
The hypotenuse has a length of 5. |
Visual Representation and AI
AI’s ability to create and manipulate visual representations significantly enhances its capacity to tackle geometry problems. By translating abstract mathematical concepts into tangible diagrams, AI can effectively break down complex problems into more manageable components, facilitating a deeper understanding of the problem’s structure and potential solutions. This visual approach mirrors how humans often learn and solve geometric problems, leveraging the power of spatial reasoning.AI can readily process and interpret geometric information presented visually, drawing insights from diagrams, graphs, and other visual elements.
This includes identifying key shapes, relationships, and properties, and using this information to derive crucial problem details. The ability to generate and interact with visuals allows AI to explore various scenarios and configurations, a capability often lacking in traditional problem-solving methods.
AI-Generated Geometry Diagrams
AI algorithms can automatically generate interactive geometry diagrams based on problem descriptions. These diagrams can dynamically adjust as parameters change, enabling exploration of different scenarios and providing visual feedback on the impact of alterations. This dynamic interaction allows for a deeper understanding of the problem’s components and how they relate to one another. For instance, an AI tool could construct a triangle, allowing users to modify side lengths or angles, and observe how these changes affect the area or other properties.
Utilizing 2D and 3D Visualizations
AI can leverage 2D and 3D visualizations to aid in geometric problem-solving. In 2D, AI can construct accurate representations of shapes, such as polygons and circles, and highlight key features, such as angles and lengths. These visualizations can be used to identify patterns, symmetries, and relationships within the problem. In 3D, AI can create models of geometric solids, enabling visualization of spatial relationships and calculations involving volume and surface area.
A practical example includes an AI tool generating a 3D model of a complex polyhedron, allowing users to explore its properties from various angles.
Dynamic Geometry Software and AI
Dynamic geometry software provides an interactive platform for exploring geometric concepts. AI can be integrated into such software, enabling more sophisticated problem-solving capabilities. This integration could involve automated generation of diagrams, interactive manipulation of geometric elements, and real-time calculation of derived quantities. For example, an AI-powered dynamic geometry tool could automatically calculate the area of a quadrilateral as its sides are adjusted, providing immediate visual feedback on the effect of these changes.
This interactive approach facilitates a deeper understanding of geometric principles and problem-solving techniques.
AI and Geometry Proofs
AI is rapidly transforming various fields, and geometry is no exception. AI tools can now assist in constructing geometric proofs, offering a novel approach to problem-solving. This capability promises to streamline the process, enhance understanding, and potentially uncover new insights into geometric relationships.AI systems can analyze geometric figures, identify relevant theorems, and suggest logical steps for constructing a proof.
This automation can be particularly beneficial for complex or intricate proofs, freeing up human mathematicians to focus on higher-level tasks and exploration.
AI Assistance in Proof Construction
AI tools can analyze geometric diagrams and identify crucial elements, such as angles, sides, and relationships between figures. This analysis allows the AI to suggest potential theorems or postulates that might be applicable to the given problem. By identifying these key relationships, the AI can then formulate a series of logical steps to construct a valid proof.
AI Identification of Logical Steps
AI algorithms can analyze the structure and logic of a proof, ensuring that each step follows logically from the previous ones and that no gaps in reasoning exist. This capability is particularly valuable in complex proofs where intricate chains of reasoning may be involved. The AI can identify missing steps or flawed logic, allowing for a more robust and complete proof.
This feature significantly improves the accuracy and efficiency of the proof-building process.
Examples of AI-Generated Proofs
While fully automated, complete proofs are still developing, AI can provide a structured series of steps for a given theorem. For example, in proving the Pythagorean theorem, an AI might initially identify the right triangle and the relationship between the sides. It could then suggest applying the area formulas for squares and triangles. Subsequently, it might suggest algebraic manipulation to reach the desired result.
Similar processes are applicable for proving theorems regarding triangle congruency or parallel lines.
Comparison of AI-Generated and Human-Created Proofs
| Theorem | AI Proof | Human Proof | Comparison |
|---|---|---|---|
| Pythagorean Theorem | AI might suggest steps involving the areas of squares on the sides of a right triangle, leading to the algebraic expression of the theorem. | A human proof might use a visual argument, showing the equality of areas, or a more abstract algebraic approach. | AI proofs are often more focused on the algorithmic steps, while human proofs may involve a deeper understanding of the underlying concepts and potential connections. |
| Triangle Angle Sum Theorem | AI might start with the parallel line construction, and then identify relationships between angles, eventually concluding the sum of angles. | A human proof might use a specific angle construction, involving parallel lines and alternate interior angles, leading to the result. | Both AI and human proofs will arrive at the same conclusion, but the human proof may involve a more intuitive understanding of geometric relationships. |
| Midsegment Theorem | AI would likely identify the midpoints and suggest connecting these points to form a segment parallel to the base, and then potentially invoking the triangle proportionality theorem. | A human proof might use a coordinate approach or vector analysis to prove the theorem, demonstrating the concept of midpoints and parallelism. | AI proofs are more focused on identifying the steps, while human proofs may offer more diverse approaches. |
Data Input and AI for Geometry Problems
AI systems require precise and structured data to effectively solve geometry problems. Different formats of input data can significantly impact the AI’s ability to understand and analyze the problem. This section details various input methods and their advantages, along with examples of AI interpretation.
Different Formats of Geometry Data Input
Various formats for geometry problem data can be input to AI systems, each with unique advantages and limitations. Understanding these formats is crucial for effective communication between the user and the AI.
Text Descriptions
Text descriptions are a common way to present geometry problems. The clarity and precision of the description directly influence the AI’s ability to extract relevant information. AI systems need to be trained to identify key geometrical concepts (e.g., “right triangle,” “parallel lines,” “congruent angles”) within the text.
Diagrams
Geometric diagrams provide visual representations of the problem. AI systems can utilize image processing techniques to extract information from diagrams, such as lengths of sides, angles, and relationships between shapes. Accurate and clear diagrams are essential for successful interpretation by the AI.
Combined Data Inputs
Combining text descriptions and diagrams can provide a more comprehensive understanding of the problem for AI systems. For example, a text description of a problem might be enhanced by a diagram that visually depicts the relationships between elements described in the text. This integrated approach improves the accuracy and reliability of the AI’s interpretation.
Table of Data Input Methods
| Data Format | Example | AI Interpretation |
|---|---|---|
| Text Description | “Find the area of a triangle with base 10 cm and height 5 cm.” | AI identifies “triangle,” “base,” “height,” and extracts numerical values for calculation. |
| Diagram | [Imagine a diagram of a right triangle with a hypotenuse labeled ‘c’ and two legs labeled ‘a’ and ‘b’. A scale is shown next to the diagram.] | AI processes the image to identify the right angle, length of sides, and their relationships. |
| Combined Text & Diagram | “Given the right triangle ABC with right angle at C, where AC = 3 and BC = 4. Find the length of AB.” [Image of a right triangle with labels as described in the text.] | AI combines text information with diagram data to accurately determine the length of the hypotenuse using the Pythagorean theorem. |
Limitations and Ethical Considerations

AI tools, while powerful in geometry problem-solving, are not without limitations. Their effectiveness hinges on the quality and comprehensiveness of the data they are trained on. Furthermore, these tools currently lack the nuanced understanding of geometric concepts that a human mathematician possesses, potentially leading to incorrect or incomplete solutions. Understanding these limitations is crucial for responsible use and integration into educational contexts.These limitations, combined with the growing role of AI in education, necessitate careful consideration of ethical implications.
AI-assisted problem-solving tools must be implemented thoughtfully to ensure fairness, avoid biases, and promote equitable learning opportunities for all students. Addressing these concerns is paramount for harnessing the potential of AI in geometry education while mitigating its potential drawbacks.
Potential Limitations of AI in Geometry Problem-Solving
AI models excel at pattern recognition and algorithmic problem-solving. However, their understanding of the underlying principles and reasoning behind geometric theorems often remains superficial. They may struggle with problems requiring creative solutions or those involving complex, non-standard geometric figures. Furthermore, AI’s ability to generalize and apply geometric concepts may be limited by the specific dataset used for training.
This limitation can lead to errors in problem-solving, particularly when presented with novel or uncommon configurations. This underscores the need for human oversight to validate and refine AI-generated solutions.
Ethical Considerations in AI-Assisted Geometry Problem Solving
The integration of AI into geometry education raises several ethical considerations. One key concern is the potential for AI to diminish the importance of human interaction and critical thinking in learning. Over-reliance on AI tools could hinder students’ development of problem-solving skills and geometric intuition.
Importance of Human Oversight in AI-Assisted Problem-Solving
Human oversight is crucial in AI-assisted problem-solving. Human mathematicians can evaluate AI-generated solutions, identify potential errors, and provide feedback to improve the AI’s performance. This collaborative approach ensures the accuracy and reliability of the solutions while fostering the development of essential mathematical reasoning skills in students. Human intervention can help students understand the underlying logic and intuition behind the solutions, leading to deeper learning and a better understanding of the subject matter.
Ethical Considerations List
- Bias in Training Data: AI models are trained on data, and if this data reflects existing biases, the AI may perpetuate these biases in its problem-solving approach. For instance, if the training data predominantly features Euclidean geometry problems, the AI might struggle with non-Euclidean geometries.
- Over-reliance on AI: Students might become overly reliant on AI tools, hindering the development of their own problem-solving skills and understanding of fundamental geometric concepts. This could negatively impact their ability to apply the knowledge independently.
- Transparency and Explainability: Students need to understand how AI arrives at its solutions. Black-box approaches, where the reasoning process is opaque, can hinder learning and trust. Understanding the “why” behind the solution is crucial for effective learning and problem-solving.
- Fairness and Accessibility: AI tools should be designed and implemented to ensure equitable access and avoid exacerbating existing inequalities. This includes considering the diverse learning needs and backgrounds of students, providing support for those with disabilities, and ensuring equal opportunities.
- Data Privacy and Security: The data used to train and operate AI models needs to be handled responsibly and securely. Protecting student data is critical for maintaining trust and adhering to privacy regulations.
Future Directions of AI in Geometry

The integration of AI into geometry problem-solving is poised for significant advancements in the coming years. These advancements will not only streamline the problem-solving process but also reshape how we understand and teach geometric concepts. This evolution promises a more interactive and personalized learning experience for students, fostering a deeper understanding of geometric principles.AI’s growing role in geometry is not merely about automation; it’s about augmenting human capabilities and expanding the scope of geometric exploration.
The future will see AI systems assisting with complex proofs, generating novel geometric conjectures, and providing personalized learning paths for students of varying backgrounds and learning styles.
Potential Impact on Problem Solving
AI’s ability to analyze geometric figures and extract crucial information will revolutionize how we approach geometry problems. Advanced algorithms will allow for rapid identification of patterns, relationships, and symmetries within geometric shapes. This will expedite the problem-solving process, enabling students to focus more on the underlying geometric principles rather than tedious calculations. For instance, AI tools could automatically identify congruent triangles within a complex diagram, guiding students towards the appropriate solution strategy.
New Applications and Areas of Development
AI’s potential in geometry extends beyond simple problem-solving. New applications include the development of automated theorem provers, capable of generating and verifying geometric proofs with high accuracy. AI-powered systems could also be used to create interactive geometric simulations, allowing students to manipulate shapes and observe the effects of transformations in real-time. Moreover, AI tools can be tailored to support specific geometric areas, such as computer-aided design (CAD) or robotic manipulation tasks involving geometric calculations.
AI in Geometry Education
AI tools can significantly enhance geometry education by providing personalized learning experiences. Adaptive learning platforms powered by AI can dynamically adjust the difficulty and pace of lessons based on a student’s performance, ensuring optimal learning outcomes. Interactive geometry software with AI-driven feedback mechanisms can provide immediate and targeted support to students struggling with particular concepts, leading to improved understanding and engagement.
Future Research Areas
Future research in AI for geometry will focus on developing more robust and efficient algorithms for analyzing geometric figures and generating proofs. Researchers will investigate methods for incorporating symbolic reasoning and knowledge representation within AI systems to enhance their understanding of geometric concepts. Another significant area of research will involve the development of AI-driven tools that can generate novel geometric conjectures and explore complex geometric structures.
Furthermore, studies on how AI can adapt to various geometric representations, such as 2D and 3D models, will be crucial.
Conclusive Thoughts
In conclusion, this exploration of AI’s role in geometry problem-solving reveals a powerful new approach to learning and understanding geometric concepts. By leveraging AI’s analytical capabilities, students can gain deeper insights and potentially develop innovative problem-solving strategies. While acknowledging limitations, this guide underscores the exciting future possibilities for AI in geometry education.